Proportional Betting Calculator
Conducting Single Proportion Hypothesis Tests
This online Kelly criterion calculator determines a recommended stake based on the prevailing odds and your estimated probability that the selection will win. All of the major odds formats are supported. This calculator also supports markets where a push/refund is possible as well as lay betting on a betting exchange such as Betfair. Dealing with these problems. To get around these two disadvantages, most punters adopting a level-staking strategy modify things somewhat. First, the “level-stake” becomes a “level-percentage” of their betting bank.So, for example, rather than committing to placing $50 on every bet, they commit to placing 2% of their betting bank. The Free Bet Calculator is the most advanced online sports bet calculator, allowing you to calculate the stake and profit for an extensive range of bets. All of the most popular bet types are supported, including Lucky 15, Single, Double, Accumulator, Patent and Round Robin, along with more specialised bets such as Alphabet, Magnificent 7, Union Jack, and the infamous Bookies Nightmare!
A hypothesis test of a sample proportion can help you make inferences about the population from which you drew it. It is a tool to determine what is probably true about an event or phenomena.
Testing a Proportion
For the results of a hypothesis test to be valid, you should follow these steps:
- Check Your Conditions
- State Your Hypothesis
- Determine Your Analysis Plan
- Analyze Your Sample
- Interpret Your Results
Check Your Conditions
To use the testing procedure described below, you should check the following conditions:
- Binary Outcomes - When conducting a hypothesis test for a proportion, each sample point should consist of only one of two outcomes. We often label one outcome a “success” and one outcome a “failure,” but it does not matter which of the two outcomes gets which label.
- Success-Failure Rate - Your sample size should be large enough that under the null hypothesis proportion you are likely to see at least 10 “success” and 10 “failures.” For example, if you have null hypothesis proportion with a 10% or 0.1 “success” rate, then you would need a sample of 100 [10 = 100 * 10%] to have a large enough sample to meet this condition. This condition helps ensure that the sampling distribution from which you collect your sample reasonably follows the Normal Distribution.
- Simple Random Sampling - You should collect your sample with simple random sampling. This type of sampling requires that every occurrence of a category or event in a population has an equal chance of being selected when taking a sample.
- Sample-to-Population Ratio - The population should be much larger than the sample you collect. As a rule-of-thumb, the sample size should represent no more than 5% of the population.
State Your Hypothesis
You must state a null hypothesis and an alternative hypothesis to conduct a hypothesis test for a proportion.
The null hypothesis, is a skeptical claim that you would like to test. It is defined by a hypothesized proportion, which is often labeled P0.
The alternative hypothesis represents an alternative claim to the null hypothesis.
Your null hypothesis and alternative hypothesis should be stated in one of three mutually exclusive ways listed in the table below.

| Null Hypothesis | Alternative Hypothesis | Number of Tails | Description |
|---|---|---|---|
| P = P0 | P ≠ P0 | Two | Tests whether the population defined by the proportion, P, from which you drew your sample is different from the population defined by the null hypothesis's proportion, P0. |
| P ≤ P0 | P > P0 | One (right) | Tests whether the population defined by the proportion, P, from which you drew your sample is greater than the population defined by the null hypothesis's proportion, P0. |
| P ≥ P0 | P < P0 | One (left) | Tests whether the population defined by the proportion, P, from which you drew your sample is less than the population defined by null hypothesis's proportion, P0. |
Determine Your Analysis Plan

Before conducting a hypothesis test, you must determine a reasonable significance level, α, or the probability of rejecting the null hypothesis assuming it is true. The lower your significance level, the more confident you can be of the conclusion of your hypothesis test. Common significance levels are 10%, 5%, and 1%.
To evaluate your hypothesis test at the significance level that you set, consider if you are conducting a one or two tail test:
- Two-tail tests divide the rejection region, or critical region, evenly above and below the null distribution, i.e. to the tails of the null sampling distribution. For example, in a two-tail test with a 5% significance level, your rejection region would be the upper and lower 2.5% of the null distribution. An alternative hypothesis of P ≠ P0 requires a two-tail test.
- One-tail tests place the rejection region entirely on one side of the null distribution i.e. to the right or left tail of the null sampling distribution. For example, in a one-tail test evaluating if the sampling distribution is above the null sampling distribution with a 5% significance level, your rejection region would be the upper 5% of the null distribution. P > P0 and P < P0 alternative hypotheses require one-tail tests.
The graphical results section of the calculator above shades rejection regions blue.
Analyze Your Sample
After checking your conditions, stating your hypothesis, determining your significance level, α, and collecting your sample, you are ready to analyze your hypothesis.
Sample proportions follow the Normal Distribution with the following parameters (i.e. numbers that define the distribution):
- The Population Proportion, P - The population proportion is assumed to be the proportion given by the null hypothesis in a single proportion hypothesis test.
- The Standard Error, SE - The standard error can be computed as follows: SE = sqrt((P x (1 - P))/ n), with n being the sample size. It defines how sample proportions are expected to vary around the null hypothesis's proportion given the sample size and under the assumption that the null hypothesis is true.
In a single proportion hypothesis test, we calculate the probability that we would observe the sample proportion, p, assuming the null hypothesis is true, also known as the p-value. If the p-value is less than the significance level, then we can reject the null hypothesis.
You can determine a precise p-value using the calculator above, but we can find an estimate of the p-value manually by calculating the z-score as follows: z = (p - P) / SE
The z-score is a test statistic that tells us how far our observation is from the null hypothesis's proportion under the null distribution. Using any z-score table, we can look up the probability of observing the results under the null distribution. You will need to look up the z-score for the type of test you are conducting, i.e. one or two tail. A hypothesis test for a proportion is sometimes known as a z-test because of the use of a z-score in analyzing results.
If we find the probability is below the significance level, we reject the null hypothesis.
Interpret Your Results
Odds Calculator Betting
The conclusion of a hypothesis test for a proportion is always either:
- Reject the null hypothesis
- Do not reject the null hypothesis
If you reject the null hypothesis, you cannot say that your sample proportion is the true population proportion. If you do not reject the null hypothesis, you cannot say that the null hypothesis is true.
A hypothesis test is simply a way to look at a sample and conclude if it provides sufficient evidence to reject the null hypothesis.
Example: Hypothesis Test for a Proportion
Let’s say you are the Marketing Director of a software company. You have set up a demo request page on your website, and you believe that 40% of visitors to that page will request a demo.
You decide to test your claim that 40% of visitors to the demo page will request a demo. So, you decide to run a hypothesis test for a proportion with a sample size of 500 visitors. Let’s go through the steps you would take to run the test.
- Check the conditions - Your test consists of binary outcomes (i.e. request demo and not request demo), your sample size is large enough to meet the success-failure condition but not too large to violate the sample-to-population ratio condition, and you collect your sample using simple random sampling. So, your test satisfies the conditions for a z-test of a single proportion.
- State Your Hypothesis - Your null hypothesis is that the true proportion of visitors requesting a demo equals 40%, formally stated P = 40%. Your alternate hypothesis is that the true proportion of vistors requesting a demo does not equal 40%, formally stated P ≠ 40%.
- Determine Your Analysis Plan - You believe that a 5% significance level is reasonable. As your test is two-tail test, you will evaluate if your sample proportion would occur at the upper or lower 2.5% [2.5% = 5%/2] of the null distribution.
- Analyze Your Sample - You collect your samle (which you do after steps 1-3). You find that the proportion of visitors request a demo in your sample is 44%. Using the calculator above, you find that a sample proportion of 44% would results in a z-score of 1.83 under the null distribution, which translates to a p-value of 6.79%.
- Interpret Your Results - Since your p-value of 6.79% is greater than the significance level of 5%, you do not have sufficient evidence to reject the null hypothesis.
In this example, you found that you cannot reject your original claim that 40% of your demo webpage vistors request demos. The test does not guarantee that your 40% figure is correct, but it does give you confidence that you do not have sufficient evidence to say otherwise.
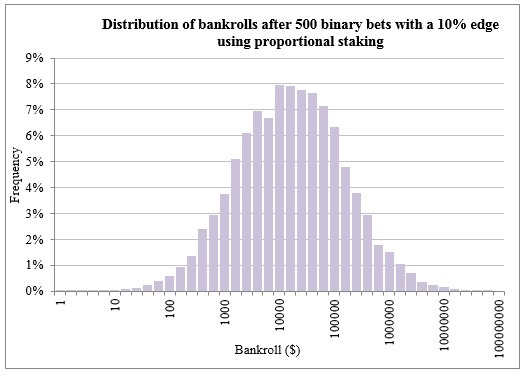
When it comes to making long-term profit through gambling, managing your betting bank correctly and finding the right staking plan is as important as identifying a winning strategy based on finding value in the market. Even if you have an edge and can identify value – which is where the bookies offer higher odds than you’d expect – you could still find yourself out of pocket with a depleted betting bank if your staking plan is not up to scratch.
Betting Unit Calculator
There are a number of different staking plans out there, all of which have their merits and downsides. Some of the most common staking systems include:
- Fixed or Level Staking where you put the same stake down regardless of the odds, such as $20 per bet whether the odds are 1.20 or 2.40
- Variable Staking where you put a stake on to win a fixed amount per bet, rather than staking a set amount, such as always ensuring your return is $20 per bet
- Percentage of Bank Staking where you bet the same percentage of your current bank balance regardless of size, for example, 5% per bet whether the bank is at $10 or $1000
- Progressive Staking where you increase or decrease the size of your stake after each bet depending on whether it won or lost, such as the Martingale System where you double up after a loss
The Kelly Criterion – also known as Kelly Strategy or Kelly Staking Plan – takes elements from Fixed, Percentage and Progressive staking to create somewhat of a hybrid staking plan. It was developed in 1956 by John Larry Kelly Jr. to identify how to maximise the long term growth rate of investments and has since been used successfully by gamblers across a range of sports and games, as well as those looking to invest in the stock market.
The Criterion looks at your current betting bank, the odds available and the edge you think you have in order to determine the optimal size of your bets. If you believe you have a significant edge on a particular bet, then your stake would be larger than a bet in which you only had a slight edge. For example, if you were and English Premiership fan betting on Tottenham to win at evens, you could place a 15% stake if you had a significant edge or a 5% stake if you had less of an edge, as calculated using the Kelly formula.
There are a number of variations of the Kelly Criterion – some of which look much scarier than others – however the one that makes most sense to me is written below. This formula is based on bets with two outcomes – i.e. you either lose all of your stake, or your stake and profit are returned if you win – although several variations have emerged for different circumstances. Luckily, there are multiple Kelly calculators online which can take away some of the pain, particularly https://www.albionresearch.com/kelly/default.php and https://bettify.com/tools/kelly.
Stake = ((Decimal Odds x % Chance Win) – 1) / (Decimal Odds – 1) * 100
Where:
Stake = Optimal size of stake
Decimal Odds = Odds offered by bookie
% Chance Win = Estimated probability of bet winning
Using the Tottenham example above, betting on Spurs to win at evens (decimal odds of 2.0) with a 53% probability and £500 bank would result in the following calculation:
Stake = ((2.0 x 0.53) – 1) / (2.0 – 1) x 100
Stake = ((1.06 – 1) / 1) x 100
Stake = 6% of bank or £30 if bank is £500
A couple of points for consideration when using the formula. If you have a zero edge – i.e. your probability is the same as the bookies’ – then the Criterion states that you should not bet. Similarly, if you have a negative edge – i.e. your probability is lower than the bookies’ – then you could either avoid the bet or you could consider laying it. It is also recommended that you don’t bet more than the calculated Kelly stake as this is known to negatively affect your bank in the long term.
The main – and somewhat significant – flaw to the Kelly Criterion is that it assumes that you know the true probability of an event happening. Whereas this is easier to ascertain when flipping a coin, it becomes near on impossible to predict for a football game involving 22 players or a horserace with 10 runners. If you cannot be sure your probabilities are entirely accurate, then this could cause detrimental effects on your bank roll, particularly if you have a habit of overestimating the likelihood of winning rather than underestimating!
Another drawback is that the percentage result from the Criterion is often a significant proportion of your bank balance, meaning that large stakes may be required. The Kelly Criterion aims to increase your betting bank at the optimal – or maximum – rate possible, which is a relatively aggressive approach. Most professional bettors would not risk anywhere near 10% of their bank on a single bet, whereas the Kelly formula rarely suggests low single digits.
A common strategy employed by some gamblers to overcome the two issues above is to use a ½ Kelly or even a ¼ Kelly strategy to ensure they are not overexposed – this is simply halving or quartering the suggested Kelly stake. With problems associated with overestimating and predicting accurate probabilities, it is always sensible to be risk averse and bet less than the Kelly amount.
Whether the Kelly Criterion is the right approach for you comes down to personal preference. It is sensible to approach your betting in a professional manner though, so concepts such as bank management and staking plans should be in your thinking while trying some of the best sports betting websites. If it’s not using Kelly, then simple concepts related to the theory such as ensuring you research your bets, creating a betting bank separate to your other accounts and eliminating emotion from any betting decisions can significantly help.